Generative Modeling of Object Keypoints
for 6D Pose Estimation

Robin Chan
rchan@techfak.uni-bielefeld.de

June 26, 2024, DataNinja sAIOnARA 2024 Conference, Bielefeld

What is 6D(oF) Pose Estimation?

  • Vision task: estimate 3D translation and 3D rotation of objects
  • Input: monocular RGB images and CAD models of objects of interest
    •


Possible Applications

  • augmented reality, autonomous vehicles, robotics, ...
  • useful when rich positional information is required
    •


  • General 3D Rotation:

$$~~~~~\mathbf{R} = \mathbf{R}_z(\alpha)\ \mathbf{R}_y(\beta)\ \mathbf{R}_x(\gamma)$$

  • Example 3D Rotation:

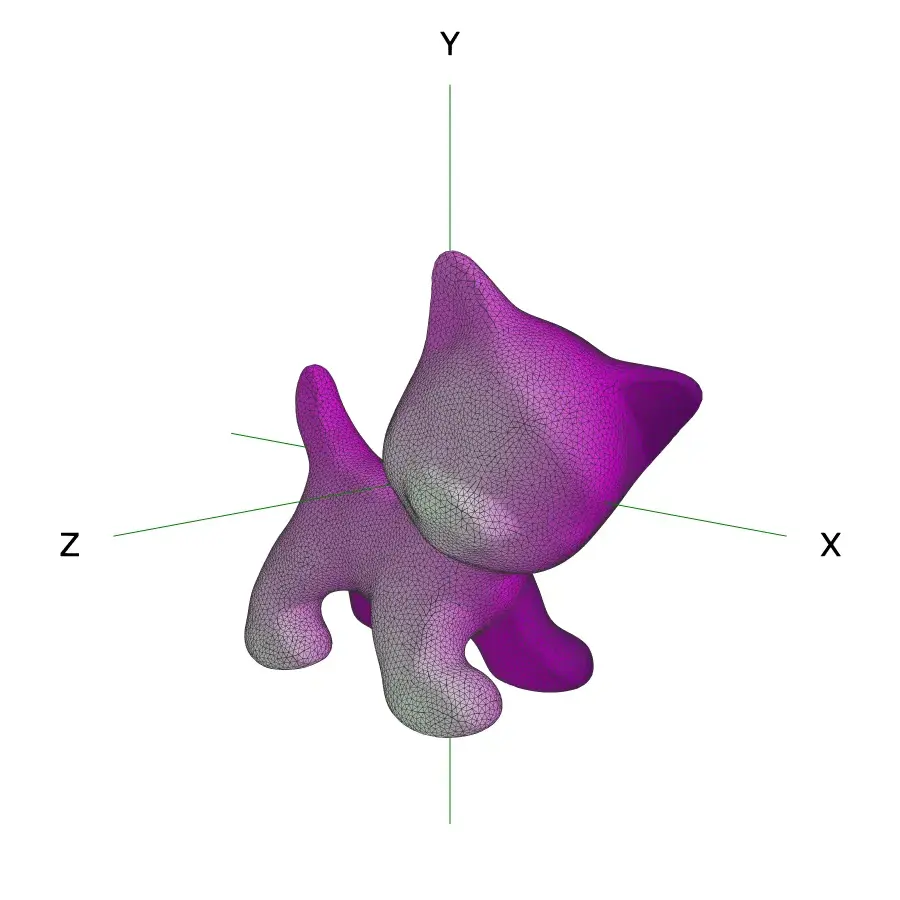
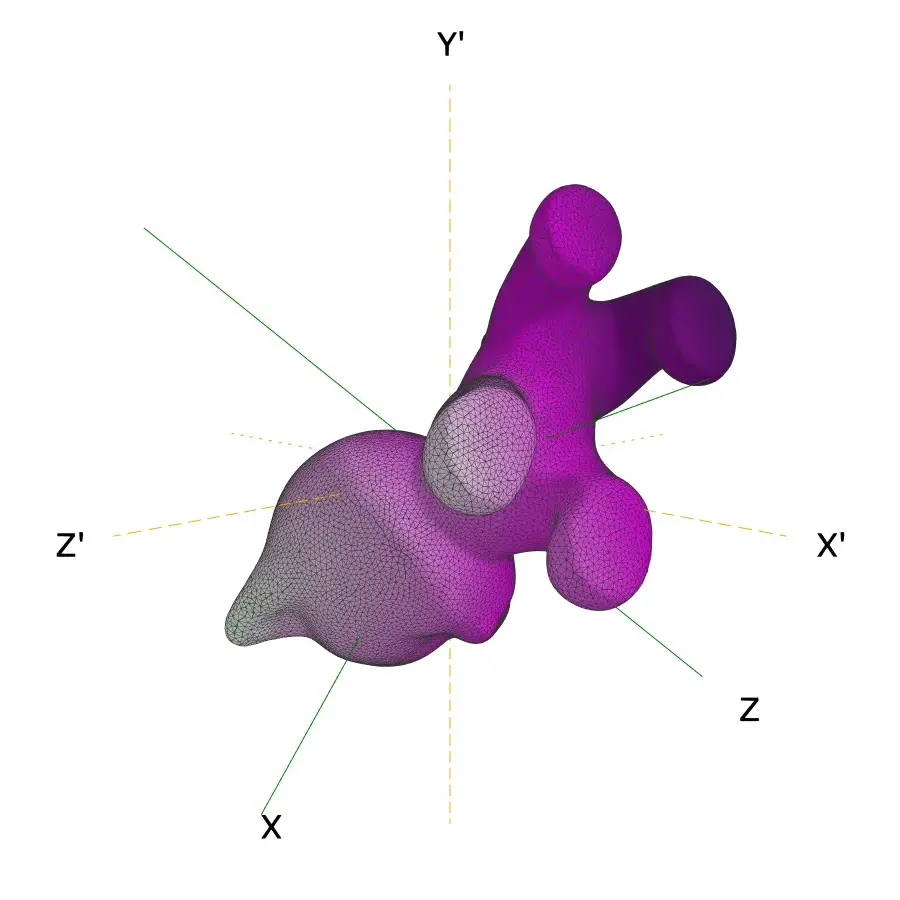$\mathbf{R} \!=~\!\!\! \begin{pmatrix} 0.11\!\! & -0.92\!\! & 0.37\! \\ -0.69\!\! & -0.39\!\! & -0.62\! \\ 0.72\!\! & -0.19\!\! & -0.67\!\end{pmatrix}$

Geometry-based Pose Estimation

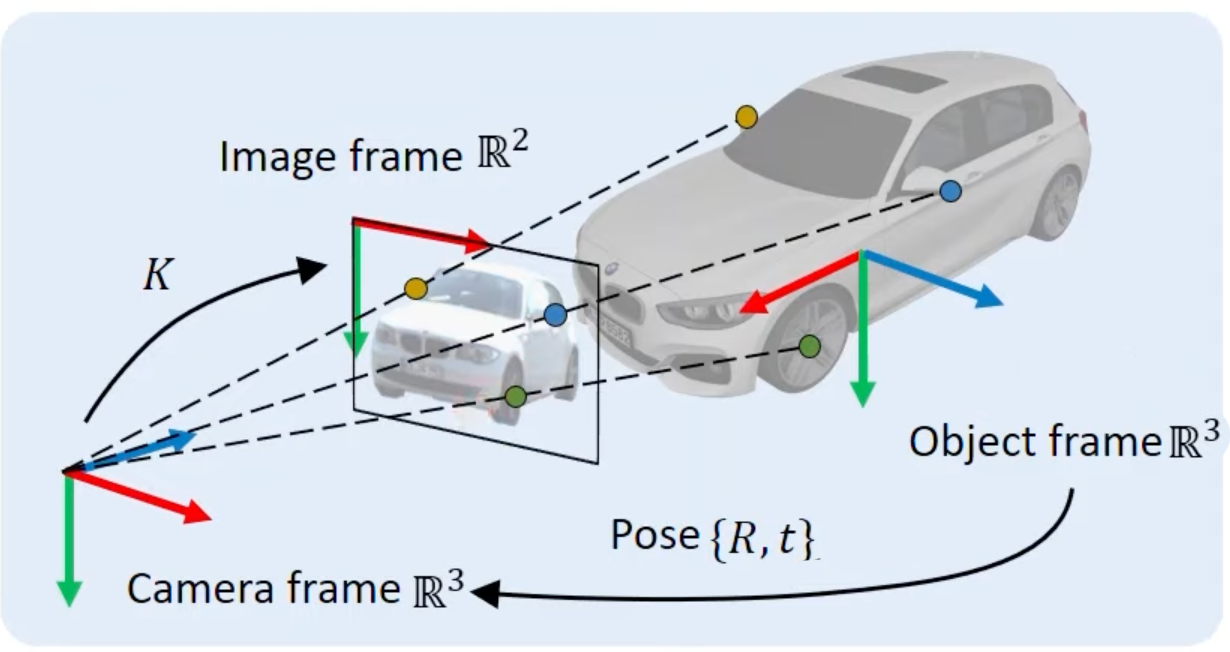
Given:
  • 2D-3D points: $\{(\mathbf{v}_i^\mathrm{2D}, \mathbf{v}_i^\mathrm{3D})\}_{i=1}^n$
  • focal length $f \in \mathbb{R}$


We can calculate:
  • rotation $\mathbf{R} \in \mathbb{R}^{3\times 3}$
  • translation $\mathbf{t} \in \mathbb{R}^3$
All points are given in their coordinate systems.
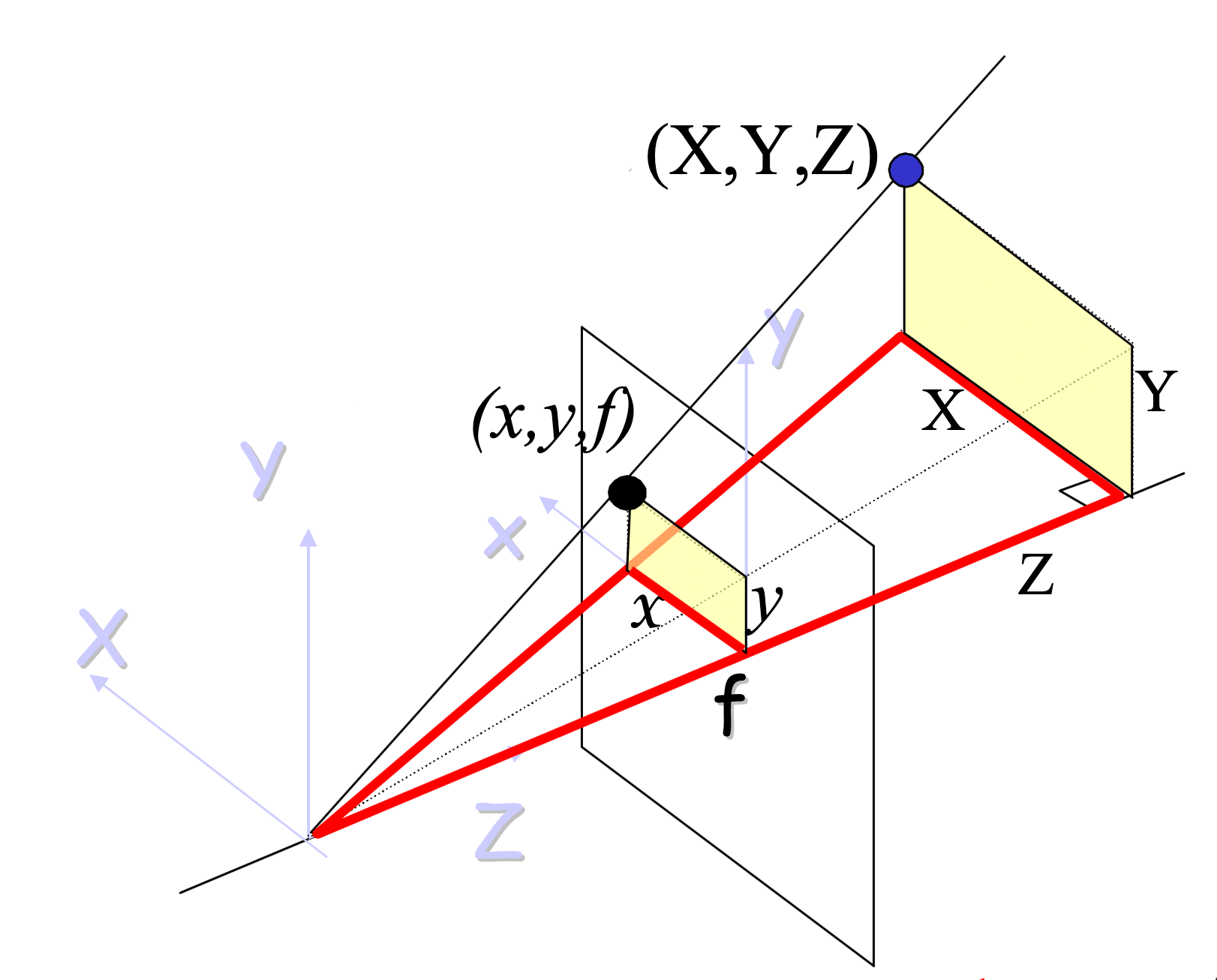
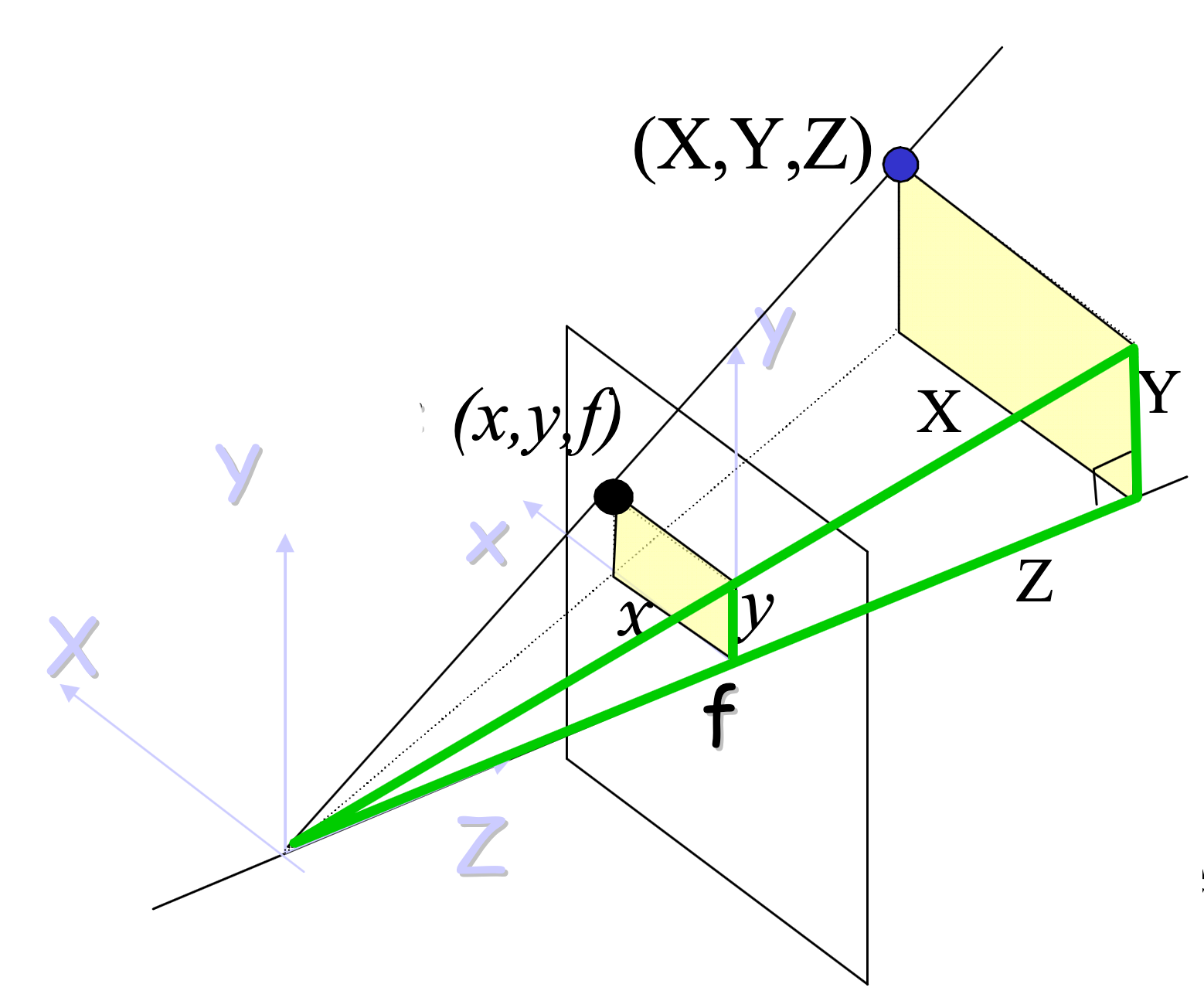
How to project 3D object points $\mathbf{v}^\mathrm{3D} = (U, V, W)^\top$ to 2D image points $\mathbf{v}^\mathrm{2D} = (x,y)^\top$?

Transform: object -> camera:
$$\begin{pmatrix} X \\ Y \\ Z\end{pmatrix} = \mathbf{R} \begin{pmatrix}U \\ V \\ W\end{pmatrix} + \mathbf{t}$$ Transform: camera -> image:
$$x=f\frac{X}{Z},~~ y=f\frac{Y}{Z}$$

Keypoint-based 6D Pose Estimation

As the 2D points are usually not known, we need to estimate their locations, e.g. with a neural network.

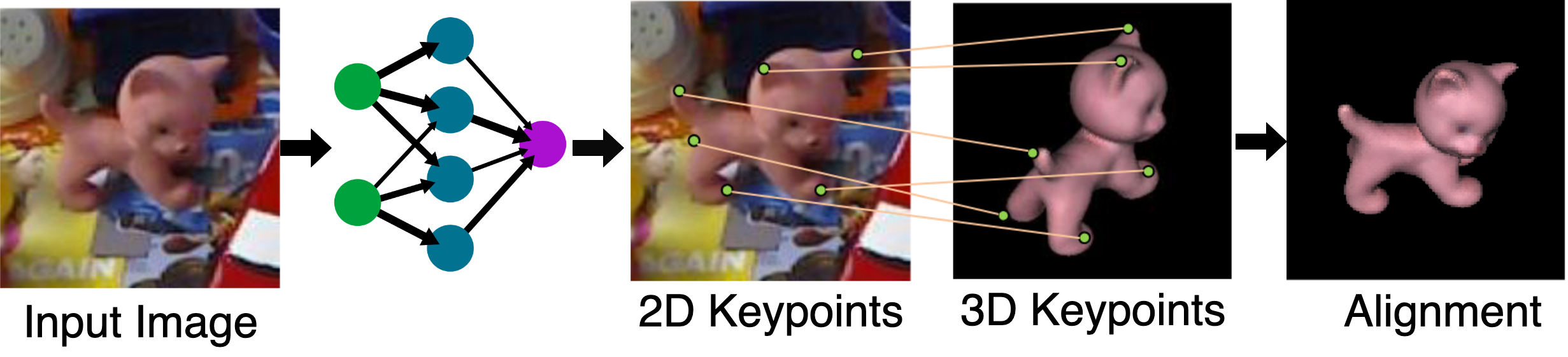
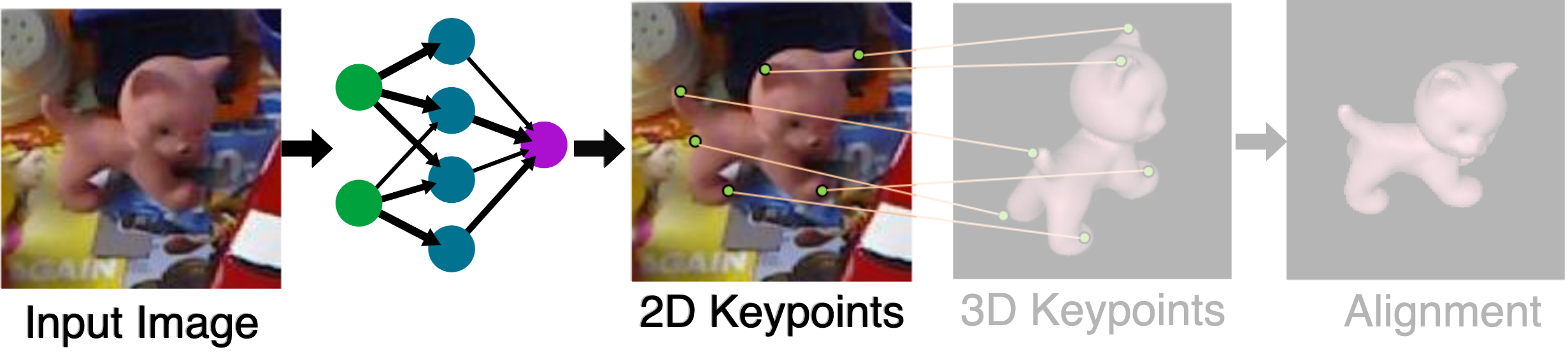
Loss function / optimization objective:
$$\mathcal{L} = \frac{1}{2} \sum_{i=1}^n \left\| \begin{pmatrix} x_i \\ y_i\end{pmatrix} - \begin{pmatrix} \hat{x}_i \\ \hat{y}_i \end{pmatrix} \right\|_2^2$$ -> minimize the reprojection error

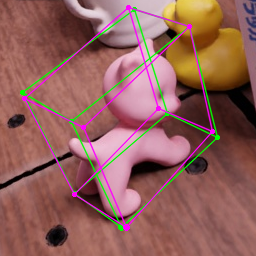
Prediction Examples

Failure Cases


Could we have identified such error...
  • ... if we had predicted entire sets of possible keypoints?
  • ... if we had information on the spatial correlation of keypoints?

Distribution of valid 2D keypoints sets

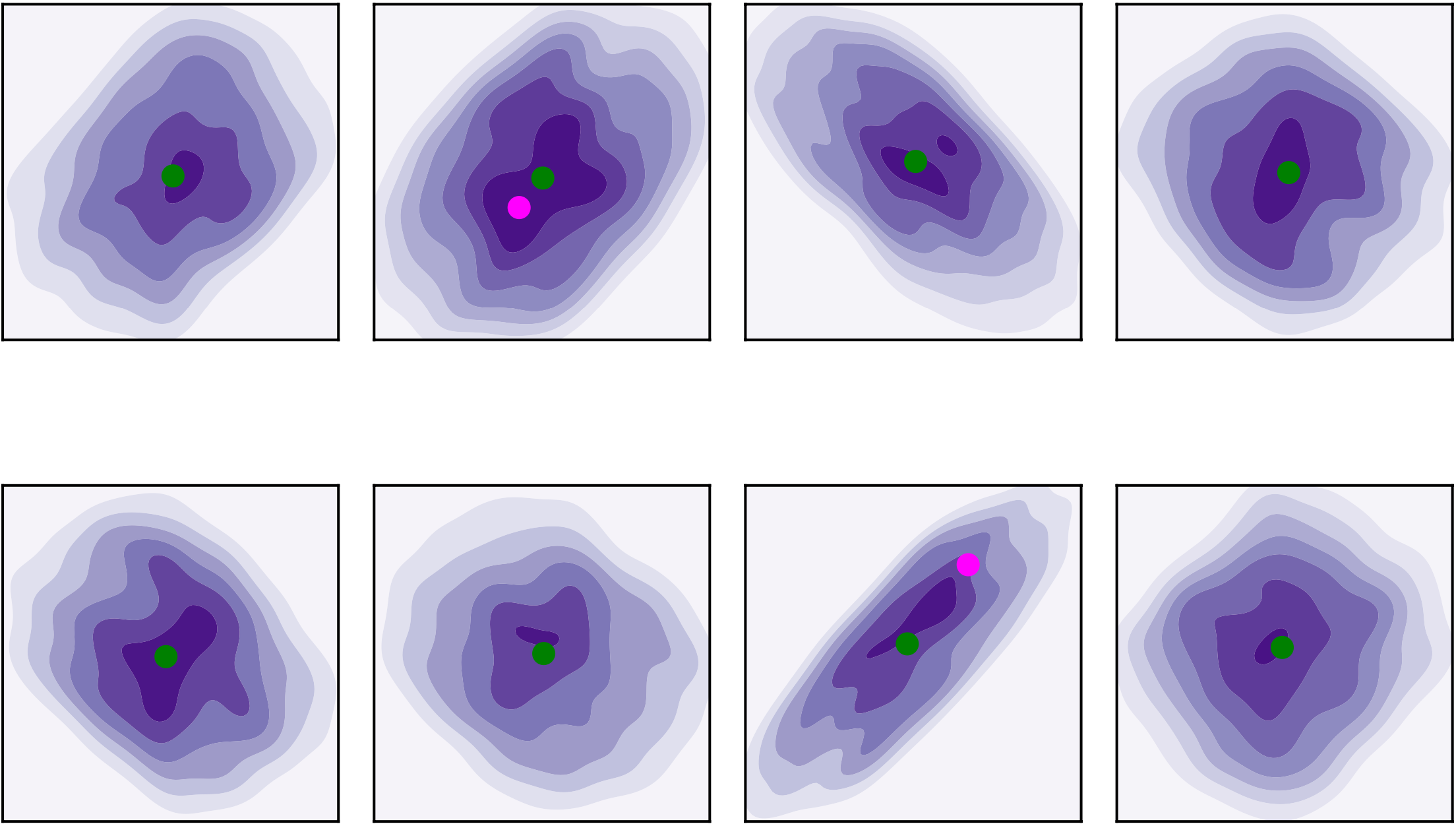
Distribution of valid 2D keypoints sets

"Ground Truth":

Distribution of valid 2D keypoints sets

"Ground Truth":
Prediction (Probabilistic) Generative Model:
    

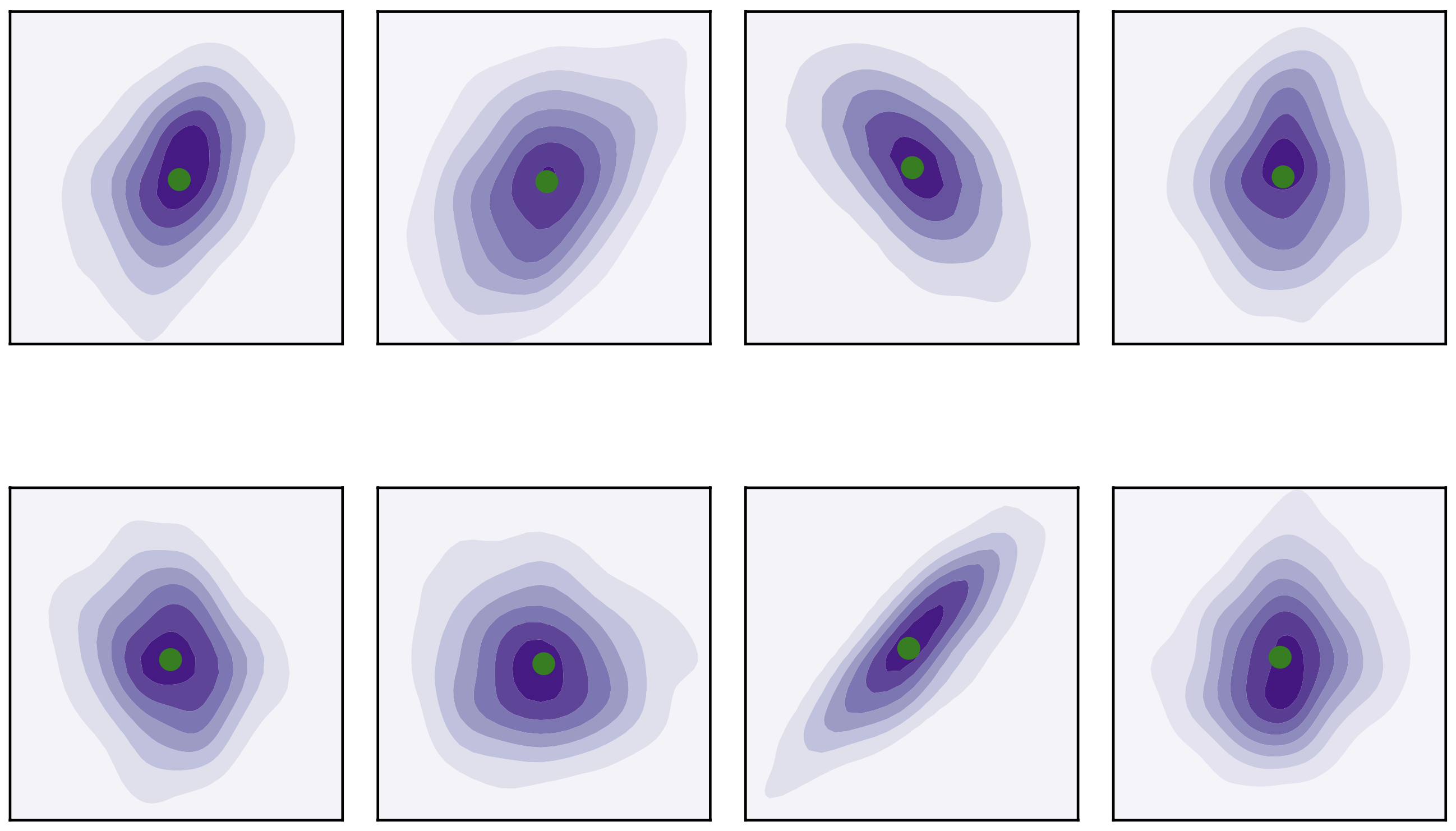
Uncertainty Quantification via Density Estimation

$$\begin{align*} \textrm{nll} &= 1578100.00 \\ \textrm{err} &= 16.37 \end{align*}$$
$$\begin{align*} \textrm{nll} &= 1376.29 \\ \textrm{err} &= 6.83 \end{align*}$$
$$\begin{align*} \textrm{nll} &= -50.14 \\ \textrm{err} &= 3.24 \end{align*}$$

Uncertainty Quantification via Density Estimation

$$\begin{align*} \textrm{nll} &= 458.27 \\ \textrm{err} &= 8.61 \end{align*}$$
$$\begin{align*} \textrm{nll} &= -37.40 \\ \textrm{err} &= 4.36 \end{align*}$$
$$\begin{align*} \textrm{nll} &= -47.55 \\ \textrm{err} &= 1.95 \end{align*}$$

Uncertainty Quantification via Density Estimation

$$\begin{align*} \textrm{nll} &= 5357.28 \\ \textrm{err} &= 8.13 \end{align*}$$
$$\begin{align*} \textrm{nll} &= -45.43 \\ \textrm{err} &= 4.71 \end{align*}$$
$$\begin{align*} \textrm{nll} &= -47.30 \\ \textrm{err} &= 2.24 \end{align*}$$

Correlation between Likelihood and Error

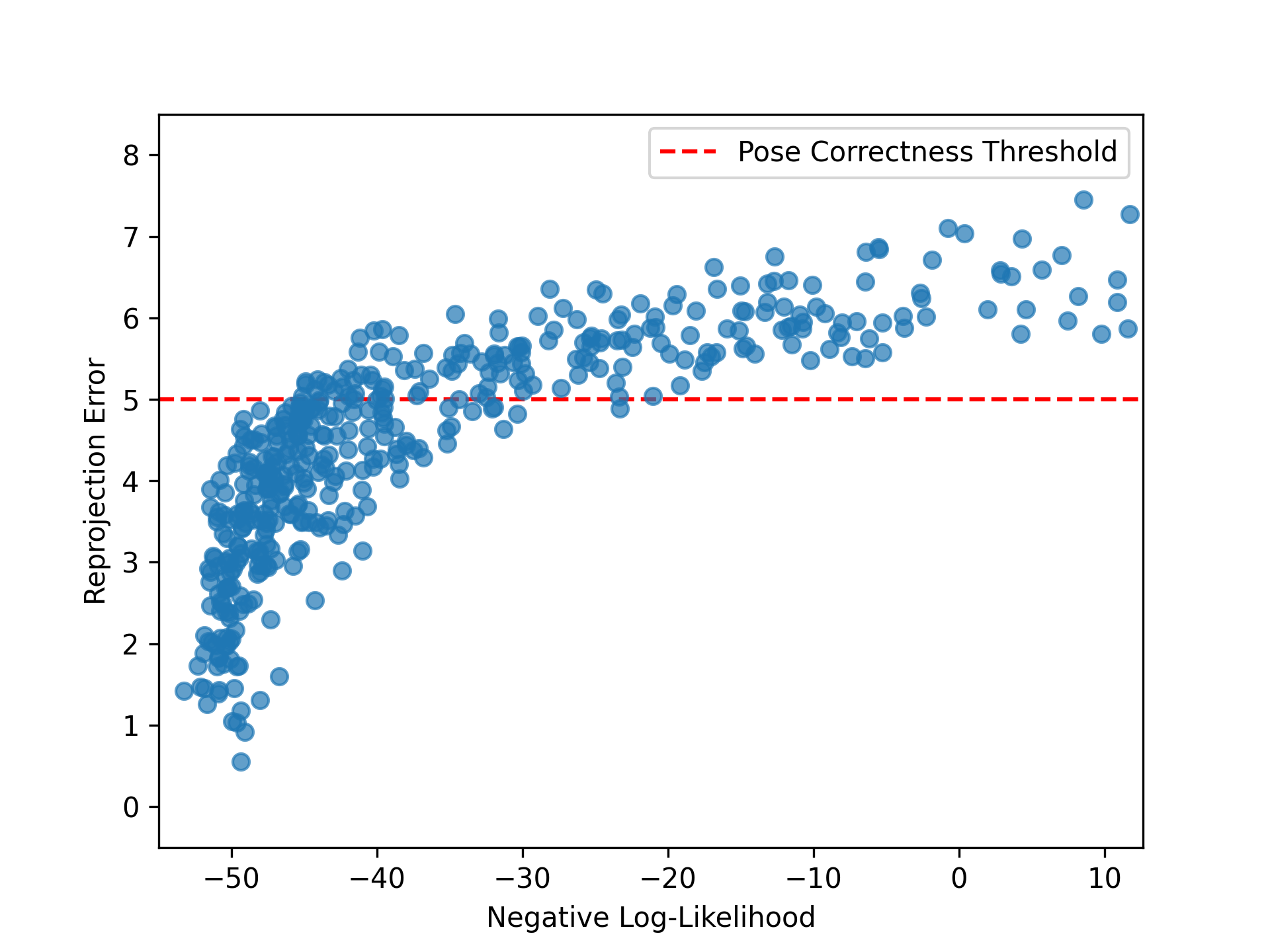
Thank you.

What are Comuter-aided Design (CAD) Models?

What are Comuter-aided Design (CAD) Models?

How to Generate CAD Models?



CAD Model generated with 3 images
from 3 different views of the object:

How to represent Rotation?

  • 2D rotation matrix:$~~\mathbf{R} = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}, \theta \in [0^\circ,360^\circ]$
  • Rotate $v = \begin{pmatrix} x \\ y\end{pmatrix}$:$~~\mathbf{R}v = \begin{pmatrix} x\cos\theta - y\sin\theta \\ x\sin\theta + y\cos\theta \end{pmatrix} = v^\prime \in\mathbb{R}^2$
  • Examples:$ \begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix}\!v~$ rotates $v$ by $180^\circ$
    $~~~~~~~~~\begin{pmatrix}\sqrt{3}/2 & -1/2 \\ 1/2 & \sqrt{3}/2\end{pmatrix}\!v~$ rotates $v$ by $30^\circ$

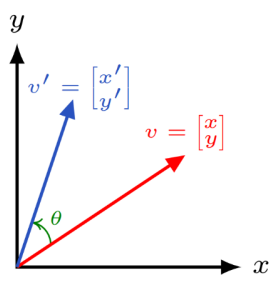
  • 3D Rotations about one axis:

$$\mathbf{R}_x(\theta) \!=\! \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix} \\ \mathbf{R}_y(\theta) \!=\!\! \begin{pmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{pmatrix} \\ \mathbf{R}_z(\theta) \!=\! \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

  • General 3D Rotation:

$$~~~~~\mathbf{R} = \mathbf{R}_z(\alpha)\ \mathbf{R}_y(\beta)\ \mathbf{R}_x(\gamma)$$

  • Example 3D Rotation:

$\mathbf{R} \!=~\!\!\! \begin{pmatrix} 0.11\!\! & -0.92\!\! & 0.37\! \\ -0.69\!\! & -0.39\!\! & -0.62\! \\ 0.72\!\! & -0.19\!\! & -0.67\!\end{pmatrix}$

What are 2D-3D Point Correspondences?

How to estimate 6D Pose with 2D Keypoints?

Projection Equations:
$$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \end{pmatrix}\! &= \mathbf{K}\mathbf{H} \begin{pmatrix} \mathbf{v}^\mathrm{3D} \\ 1\end{pmatrix} \Leftrightarrow \begin{pmatrix}x^\prime \\ y^\prime \\ z^\prime \end{pmatrix}\! = \mathbf{K}\mathbf{H} \begin{pmatrix}U \\ V \\ W \\ 1\end{pmatrix} \Leftrightarrow \\ \textcolor{black}{\begin{pmatrix}x^\prime \\ y^\prime \\ z^\prime\end{pmatrix}\!} &= \textcolor{black}{\!\begin{pmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}\! \begin{pmatrix}r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1\end{pmatrix}\! \begin{pmatrix}U \\ V \\ W \\ 1\end{pmatrix}} \\ \Rightarrow x &= \frac{x^\prime}{z^\prime},~~ y = \frac{y^\prime}{z^\prime},~~ \begin{pmatrix}x \\ y \end{pmatrix} = \mathbf{v}^\mathrm{2D} \end{align*} $$
$$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \end{pmatrix}\! &= \mathbf{K}\mathbf{H} \begin{pmatrix} \textcolor{blue}{\mathbf{v}^\mathrm{3D}} \\ 1\end{pmatrix} \Leftrightarrow \begin{pmatrix}x^\prime \\ y^\prime \\ z^\prime \end{pmatrix}\! = \mathbf{K}\mathbf{H} \begin{pmatrix}U \\ V \\ W \\ 1\end{pmatrix} \Leftrightarrow \\ \textcolor{blue}{\begin{pmatrix}x^\prime \\ y^\prime \\ z^\prime\end{pmatrix}\!} &= \textcolor{blue}{\!\begin{pmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}\! \begin{pmatrix}r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1\end{pmatrix}\! \begin{pmatrix}U \\ V \\ W \\ 1\end{pmatrix}} \\ \Rightarrow x &= \frac{x^\prime}{z^\prime},~~ y = \frac{y^\prime}{z^\prime},~~ \begin{pmatrix}x \\ y \end{pmatrix} = \textcolor{blue}{\mathbf{v}^\mathrm{2D}} \end{align*} $$
$$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \end{pmatrix}\! &= \mathbf{K}\mathbf{H} \begin{pmatrix} \textcolor{blue}{\mathbf{v}^\mathrm{3D}} \\ 1\end{pmatrix} \Leftrightarrow \begin{pmatrix}x^\prime \\ y^\prime \\ z^\prime \end{pmatrix}\! = \mathbf{K}\mathbf{H} \begin{pmatrix}U \\ V \\ W \\ 1\end{pmatrix} \Leftrightarrow \\ \textcolor{black}{\begin{pmatrix}x^\prime \\ y^\prime \\ z^\prime\end{pmatrix}\!} &= \!\begin{pmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}\! \textcolor{red}{\begin{pmatrix}r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1\end{pmatrix}\!} \textcolor{black}{\begin{pmatrix}U \\ V \\ W \\ 1\end{pmatrix}} \\ \Rightarrow x &= \frac{x^\prime}{z^\prime},~~ y = \frac{y^\prime}{z^\prime},~~ \begin{pmatrix}x \\ y \end{pmatrix} = \textcolor{blue}{\mathbf{v}^\mathrm{2D}} \end{align*} $$
Can be solved with Perspective-n-Point algorithms.
As the 2D points are usually not known, we need to estimate their locations, e.g. with a neural network.

Loss function / optimization objective:
$$\mathcal{L} = \frac{1}{2} \sum_{i=1}^n \| \mathbf{v}_i^\mathrm{2D}-\hat{\mathbf{v}}_i^\mathrm{2D} \|_2^2 ~~ \text{or}$$ $$\Leftrightarrow \mathcal{L} = \frac{1}{2} \sum_{i=1}^n \left\| \mathbf{K}\mathbf{H} \begin{pmatrix} \mathbf{v}^\mathrm{3D}_i \\ 1 \end{pmatrix} - \mathbf{K}\hat{\mathbf{H}}\begin{pmatrix} \mathbf{v}^\mathrm{3D}_i \\ 1 \end{pmatrix} \right\|_2^2$$